网络分析法
网络分析法(ANP)的前身是层次分析法(The analytic hierarchy
process,AHP)。
AHP
的核心是将系统划分层次,将同一层次的元素视为相互独立,只考虑上层元素对下层元素的支配作用。但在许多实际问题中,各层次内部元素往往是依存的,
低层元素对高层元素亦有支配作用,
即存在层间反馈,使得系统的结构更类似于网络结构,由此产生了网络分析法(ANP)。
ANP的结构分析
基本组成
ANP首先将系统元素划分为两大部分。
第一部分称为控制因素层,
包括问题目标及决策准则。所有的决策准则均被认为是彼此独立的,
且只受目标元素支配。控制因素中可以没有决策准则, 但至少有一个目
标。控制层中每个准则的权重均可用传统的AHP方法获得。
第二部分为网络层, 它是由所有受控制层支配的元素组组成的,
其内部是互相影响的网络结构, 图1即为一个典型的ANP结构。
.default}/?t=f64948a9-cced-436e-b248-ea763020fee2)
图1 典型的ANP结构
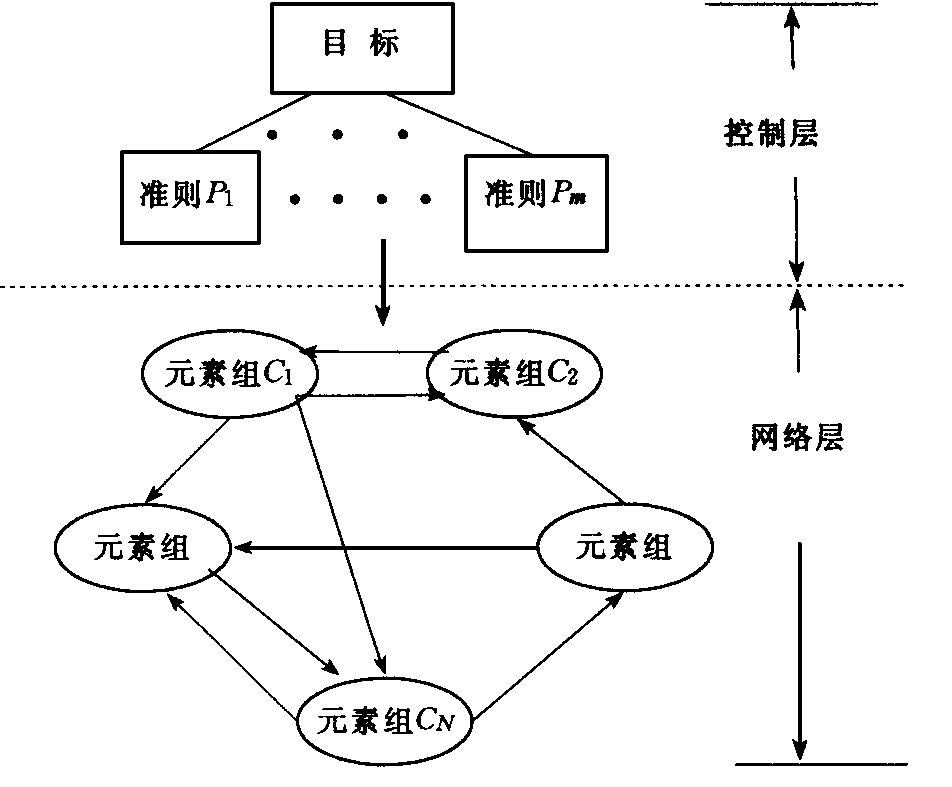
图1 典型的ANP结构
优势度
AHP的一个重要步骤就是在一个准则下, 将受支配元素两两比较,
由此获得判断矩阵。但在ANP中被比较元素之间可能不是独立的, 而是相互依存的,
因而这种比较将以两种方式进行:
- 直接优势度:元素间相互独立时,给定一个准则, 将两元素对于该准则的重要程度进行比较。
- 间接优势度:元素间相互依存时,给定一个准则, 将两个元素在准则下对第三个元素(称为次准则) 的影响程度进行比较。
ANP结构的超矩阵与加权超矩阵
设ANP的控制层中有元素p1, ⋯, pn,
网络层有元素组C1, ⋯, CN,
其中Ci中有元素ei1, ⋯, eini,
i = 1, ⋯, N。
以控制层元素Ps(s=1,⋯,m)
为准则, 以Cj中元素ejl(l=1,⋯,nj)为次准则,元素组Ci中元素按其对ejl的影响力大小进行间接优势度比较,
即Ps下构造判断矩阵:
.default}/?t=b421431d-9a0c-43fe-9b62-3bc7d1bf250f)
记Wij为
$$
\begin{bmatrix}
\quad\omega_{i1}^{(j1)} & \quad\omega_{i1}^{(j2)} & \quad\cdots
& \quad\omega_{i1}^{(jn_j)}\quad \\
\quad\omega_{i2}^{(j1)} & \quad\omega_{i2}^{(j2)} & \quad\cdots
& \quad\omega_{i2}^{(jn_j)}\quad \\
\vdots & \vdots & \ddots & \vdots \\
\quad\omega_{in_i}^{(j1)} & \quad\omega_{in_i}^{(j2)} &
\quad\cdots & \quad\omega_{in_i}^{(jn_j)}\quad \\
\end{bmatrix}
$$
这里Wij的列向量就是Ci中元素ei1, ⋯, eini对Cj中元素ej1, ⋯, ejnj的影响程度排序向量。若Cj中元素不受Ci中元素影响,则Wij = 0。这样最终可获得Ps下,
超矩阵W: $$
W=\begin{array}{lc}
\mbox{}&
\begin{array}{cccccccccc}
1 & \cdots & n_1 & 1 & \cdots & n_2 & \cdots
& 1 & \cdots & n_N
\end{array}\\
\begin{array}{c}
1 \\ \vdots \\ n_1 \\
1 \\ \vdots \\ n_2 \\
\vdots \\
1 \\ \vdots \\ n_N
\end{array} & \left[\begin{array}{cccc}
\quad W_{11} & \qquad W_{12} & \quad\cdots & \quad W_{1N} \\
\\
\vdots \\
\\
\quad W_{21} & \qquad W_{22} & \quad\cdots & \quad W_{2N} \\
\\
\\
\vdots \\
\\
\quad W_{N1} & \qquad W_{N2} & \quad\cdots & \quad W_{NN}
\end{array}\right]
\end{array}
$$ 这样的非负超矩阵共有m个, 其子块Wij是列归一化的,
但W却不是列归一化的。为此以Ps 为准则,
对Ps下各组元素对准则Cj(j=1,⋯,N)的重要性进行比较。
.default}/?t=ece8a2b7-ce05-4f56-b1ba-1122255c00a7)
与CJ无关的元素组对应的排序向量分量为零,由此得加权矩阵
$$
\left[
\begin{matrix}
a_{11} & a_{12} & \cdots & a_{1N} \\
a_{21} & a_{22} & \cdots & a_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
a_{N1} & a_{N2} & \cdots & a_{NN} \\
\end{matrix}
\right]
$$ 对超矩阵w的元素加权,得$\bar{W}=\bar{(W_{ij})}$,其中 $$
\bar{(W_{ij})} = a_{ij}W_{ij},\quad i=1,\cdots,N \quad j=1,\cdots,N
$$ W̄为加权超矩阵,其列和为1,称为列随机矩阵。为简单起见以下的超矩阵均为加权超矩阵,并仍用符号W表示。
极限相对排序向量
设(加权)超矩阵W的元素为Wij,则Wij的大小反映了元素i对元素j的一步优势度。考虑到i对j的优势度还可根据
$$
\sum_{k=1}^N \omega_{ik}\omega_{kj}
$$ 其结果被称为二步优势度,是W2的元素,且W2仍为列归一化。
当下式存在时 W∞ = limt → + ∞WtW∞的第j列就是Ps下网络层中各元素对于元素j的极限相对排序向量。
主要ANP结构的超矩阵
内部独立的递阶层次结构
.default}/?t=c93dd834-9dfd-4f48-971a-15117dee551f)
图2 内部独立的循环系统超矩阵
此时可把目标层C1看作既属于控制层又属于网络层元素(图), C1下超矩阵为 $$
W=\left[
\begin{matrix}
0 & & \\
W_{21} & 0 & \\
& W_{32} & \\
& & \ddots \\
\end{matrix}
\right]
$$
内部依存的递阶层次结构
.default}/?t=6cd632c4-4af2-4b07-bb30-c5f728c86d6f)
图3 内部依存的循环系统
控制层C1仍作为网络层的一部分,其超矩阵为
$$
W=\left[
\begin{matrix}
W_{11} & & & \\
W_{21} & W_{22} & & \\
& W_{32} & \ddots & \\
& & \ddots & \ddots\\
& & W_{NN-1} & W_{NN}\\
\end{matrix}
\right]
$$
内部独立的循环系统超矩阵
.default}/?t=1e2e1fde-41bd-4182-9227-173b0b40e242)
图4 内部独立的循环系统
其结构如图所示,W是不可约非负矩阵,最大特征值λ = 1是单根,但除1外还有其它模为1的特征根
$$
W=\left[
\begin{matrix}
0 & & & W_{N} \\
W_{1} & 0 & & \\
& W_{ 2} & \ddots & \\
& & \ddots & \ddots\\
& & W_{N-1} & 0 \\
\end{matrix}
\right]
$$
内部依存的循环系统
.default}/?t=eff25815-c27c-477a-97b1-e3ac617fbc9e)
图5 内部依存的循环系统
其超矩阵为 $$
W=\left[
\begin{matrix}
W_{11} & W_{12} & \cdots & W_{1N} \\
W_{21} & W_{22} & \cdots & W_{2N} \\
& & \vdots & \\
W_{N1} & W_{N2} & \cdots & W_{NN} \\
\end{matrix}
\right]
$$
一般网络结构
由于一般网络结构(图) 总可将元素划分为控制层和网络层两大层次,
而任何网络层均可看成内部依存的结构,故经过适当简化总可转化为上述几种情形之一进行处理。
例题求解
题目综述
考虑成本、维修和耐用性三个方面,在美国车、日本车以及欧洲车之间进行选择。其中,成本、维修和耐用性之间相互影响,已知三者的权重矩阵如下:
ㅤ | 成本 | 维修 | 耐用性 |
成本 | 0.3 | 0.2 | 0.6 |
维修 | 0.4 | 0.25 | 0.3 |
耐用性 | 0.3 | 0.55 | 0.1 |
一致性指标说明
- 当判断矩阵具有完全一致性时,一致性指标CI=0
- 当判断矩阵具有满意一致性时,需引入判断矩阵的平均随机一致性指标RI值。对于1-9阶判断矩阵,RI值如下:
阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
RI | 0 | 0 | 0.58 | 0.8 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
- 当$CR=\frac{CI}{RI}<0.10$时,认为判断矩阵具有满意的一致性,否则需要调整判断矩阵
- 引入判断矩阵最大特征根以外的其余特征根的负平均值,作为度量判断矩阵偏离一致性的指标,即用$CI=\frac{\lambda_{max}-n}{n-1}$检查决策者思维的一致性。CI值越大,表明判断矩阵偏离完全一致性的程度越大;CI值越小(接近于0),表明判断矩阵的一致性越好。
ANP求解
问题抽象为ANP结构如图[^5]
.default}/?t=af55d49b-d006-4b04-87a6-0ddf30f430b7)
图6 例题对应ANP结构
首先写出三种因素:成本、维修和耐用性对于三类车辆的判断矩阵,并求出对应特征向量与随机一致性比率CR。
.default}/?t=95c5faa1-bc1a-47b9-bcf3-ef0b99eeb6ae)
接着,考虑题中给出的成本、维修和耐用性之间的相互影响,得到初始超矩阵如下表:
.default}/?t=648d1ee7-b87c-4bbf-a51e-40ee65ee4ef3)
假定加权矩阵A如下,可得到对应的加权超矩阵表 $$
A=\left[
\begin{matrix}
0.5 & 1 \\
0.5 & 0 \\
\end{matrix}
\right]
$$
将加权超矩阵稳定处理,即自乘4-6次,得到稳定的极限超矩阵。(注意,每一步自乘之前需要将列向量归一化,否则加权超矩阵会越变越小,不会收敛)
.default}/?t=459b4724-7e63-4bee-898f-2ff8731bef12)
ANP决策结果表明:美国车是最优选择,成本是决定性因素。
修改记录
- 2022-08-21, @杜劲达重新整理
- 2020-12-10, @刘哲恺重新整理
- 2018-01-28, @李婧松 吴娴 王浥清创建初始页面
参考文献
- Abraham Charnes, William W Cooper, and Edwardo Rhodes. Measuring the efficiency of decision making units. European journal of operational research, 2(6):429–444, 1978.↩︎